Bucket Sorting

Explanation of bucket sorting

Simple Version

To start with, assuming we have this set of numbers and we want to sort it in inscending order:

1
The original set of number: 3,3,6,5,2,1,7
1
The result set of number: 1,2,3,3,5,6,7

To use bucket sort to finish this task, firstly we need to build buckets to contain the numbers. Note that the amount of buckets depends on the range of set:

Then for each number in the set, we compare it with the number on each bucket from left to right, if they are same, the amount of number in the bucket increase by 1:

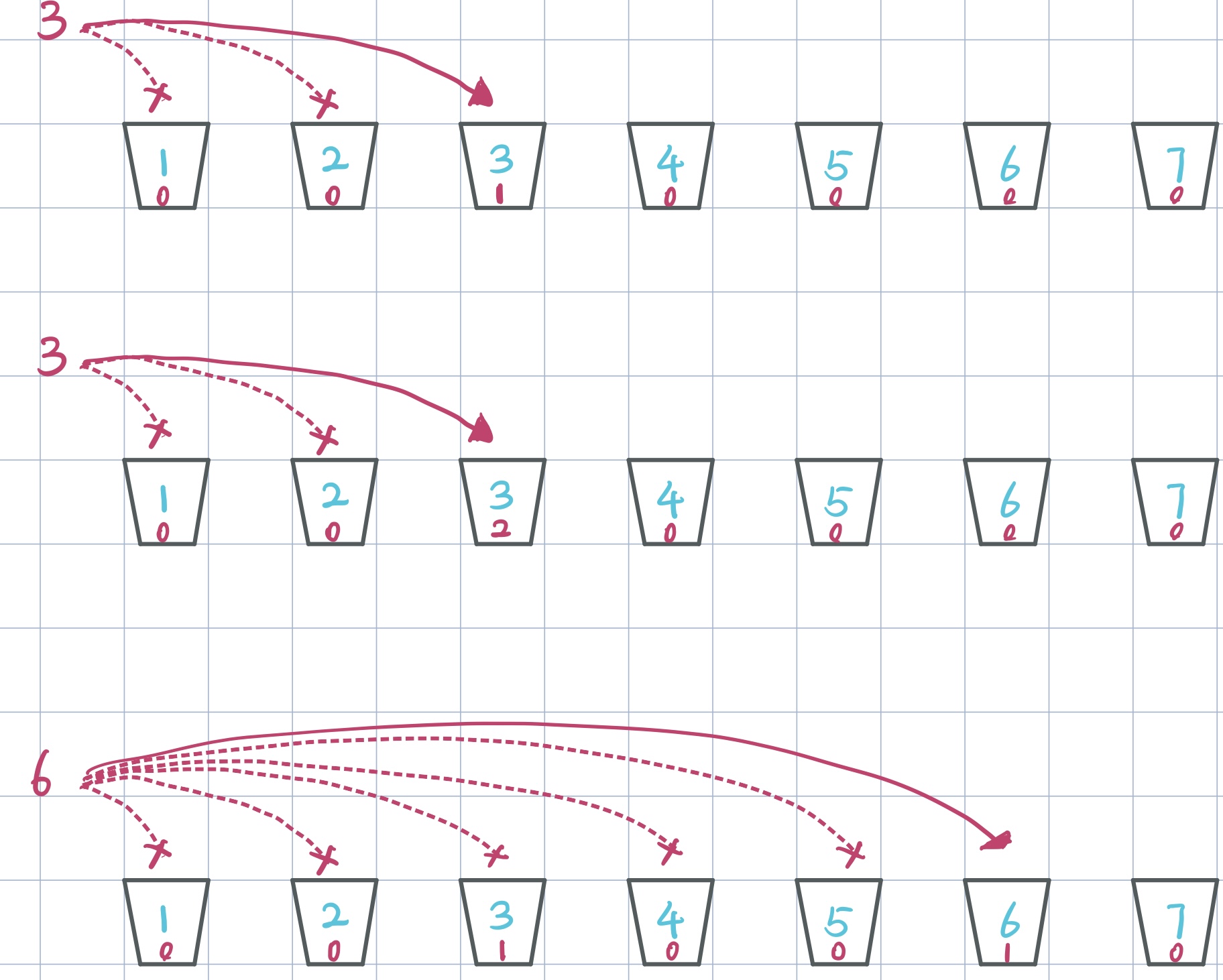
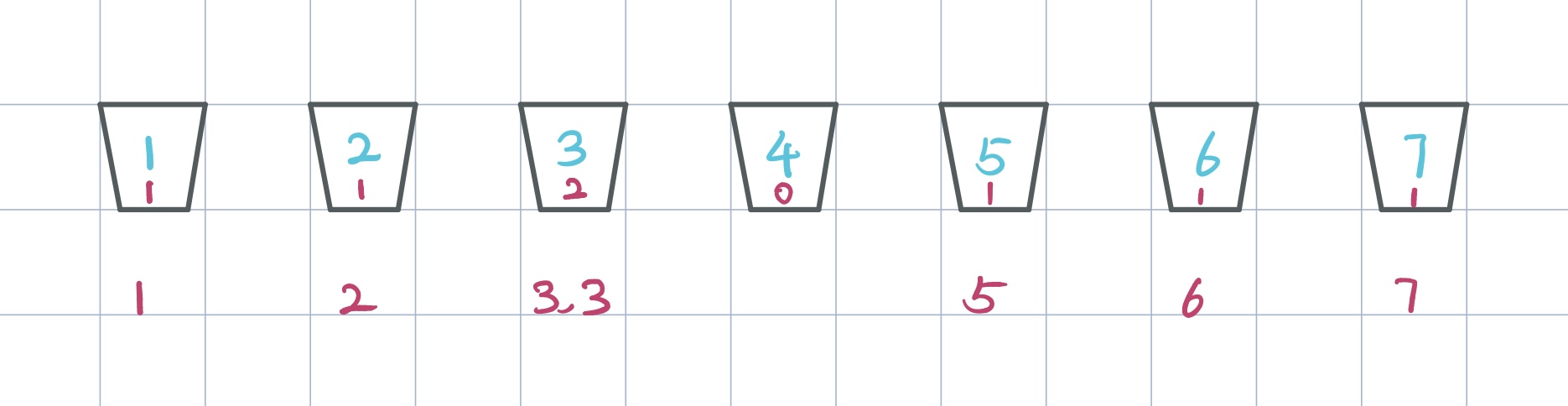
After we have put all numbers in the corresponding buckets, we travel buckets from left to right to see how many numbers in each buckets and pick them out one by one. The numbers are sorted:

Universal Version

In the last version, we have a empty bucket unused which causes waste of money. How can we avoid this kind of waste?

We can not save it completly, but we can improve the use efficency of buckets. Consider that the number on each bucket is a range instead of certain number: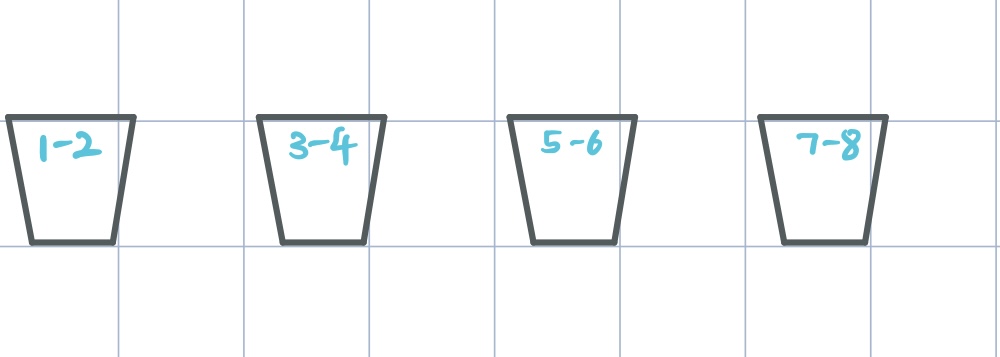

In this case, for each number in the set, we compare it with the range on each bucket from left to right, if the number is contains in the range, put the number in the bucket. Note that the numbers in the buckets must keep inscending order(can use insertion sort, another is also ok):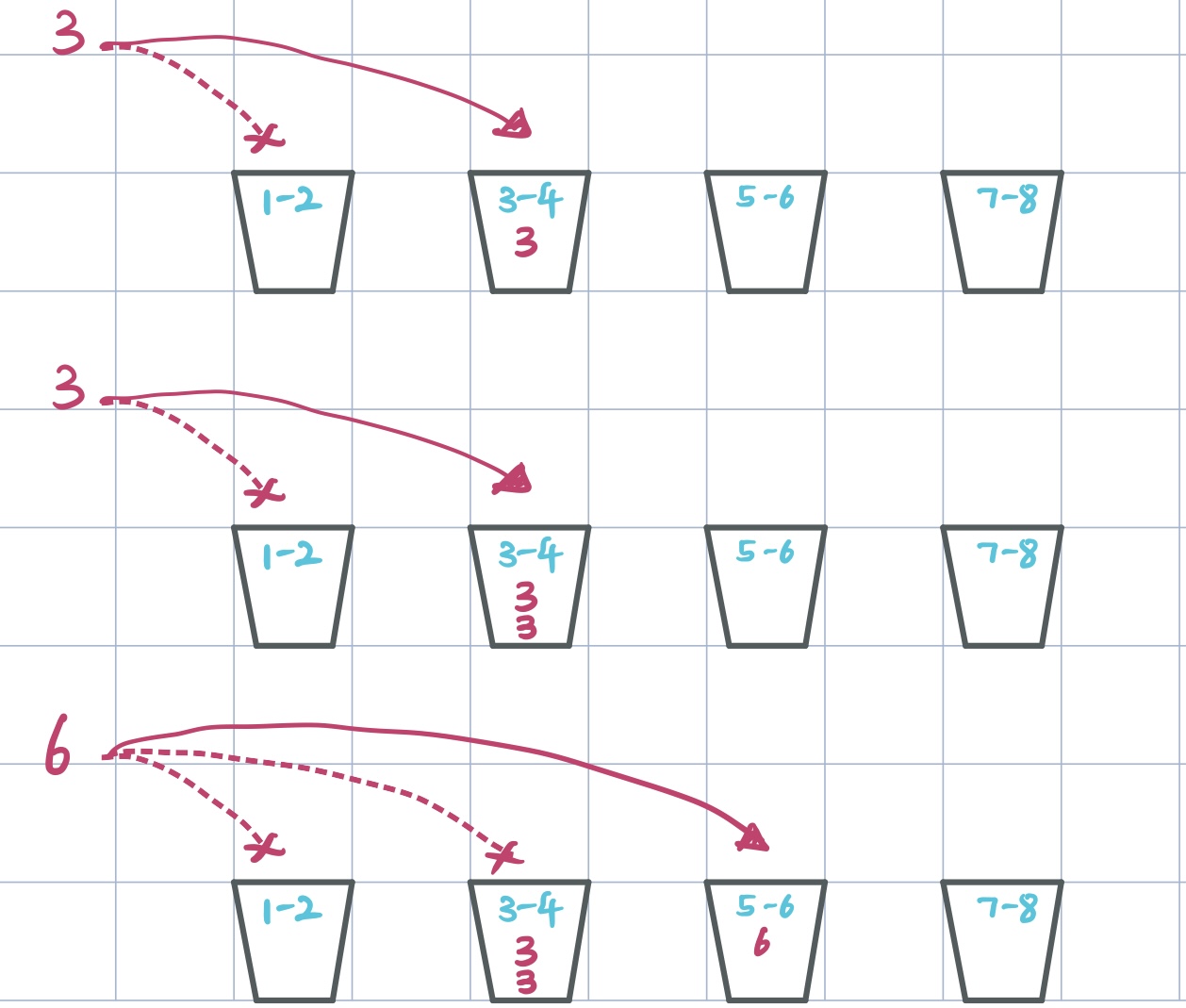

Then we travel buckets from left to right to see how many numbers in each buckets and pick them out in order. The numbers are sorted: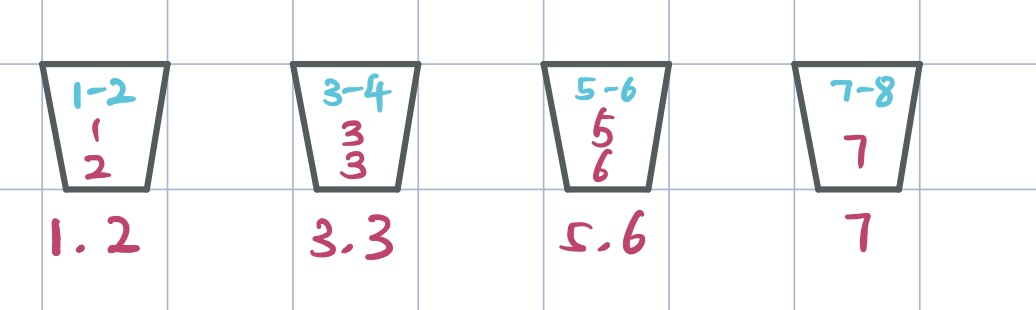

You may notice that the choice of range is important. If the range is too small, the space cost is large. If the range is too large, the time cost is large.

Pros and cons of bucket sorting

Pros

  1. The time complexity is about O(n). The exact one is O( n* m ), m is the time complexity of the sort inside the bucket. The efficiency is high.

    Cons

  2. When the data is not homogenous, the efficiency decrease. If the data is exact concertrate, the bucket sort may decrease to the sort inside the bucket.
  3. A bad choice of range can also cause the efficiency decrease or the waste of space. The algorithm is sensed to choice of range.

    Implementation

    Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def bucketSort(list):
    minNum = min(list)
    maxNum = max(list)
    buckets = []
    for i in range(minNum,maxNum+1,2):
        buckets.append([])
    for num in list:
        index = (num-minNum)//2
        buckets[index].append(num)
        buckets[index].sort()
    for bucket in buckets:
        for num in bucket:
            print(num)

bucketSort([3,3,6,5,2,1,7])

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import java.util.*;
class Buckets{
    public int min;
    public int max;
    ArrayList<ArrayList<Integer>> buckets = new ArrayList<ArrayList<Integer>>();
    public Buckets(int min,int max){
        for (int i = min;i<=max;i+=2){
            buckets.add(new ArrayList<Integer>()); 
        }
        this.min = min;
        this.max = max;
    }
    public void fillBucket(int n){
        int index = (n-this.min)/2;
        this.buckets.get(index).add(n);
        Collections.sort(this.buckets.get(index));
    }
    public ArrayList<Integer> getAllNums(){
        ArrayList<Integer> ans = new ArrayList<Integer>();
        for(ArrayList<Integer> bucket:this.buckets){
            for(int num:bucket){
                ans.add(num);
            }
        }
        return ans;
    }
}
public class BucketSort {
    public static void main(String[] args) { 
        int[] list = {3,3,6,5,2,1,7};
        Buckets buckets = new Buckets(1, 7);
        for(int num:list){
            buckets.fillBucket(num);
        }
        ArrayList<Integer> ans = buckets.getAllNums();
        System.out.println(ans);
    }
}